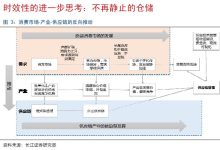
如何确定合适的温度范围与比例尺
一、引言
在日常生活中,我们经常会遇到需要确定合适温度范围和比例尺的情况。
无论是在烹饪、工业生产、科学实验还是建筑设计等领域,准确把握温度范围和比例尺都至关重要。
本文将详细介绍如何确定合适的温度范围和比例尺,以帮助读者更好地应对各种实际场景。
二、确定合适的温度范围
1. 明确需求:首先要明确所需温度范围的具体应用场景,如烹饪、养殖、工业生产等。不同场景对温度的要求会有所不同,因此需针对不同场景进行温度范围的设定。
2. 参考标准:参考相关行业标准、规范或经验数据,了解所需温度范围的一般值。这些标准或数据可以为我们提供一个基本的参考依据。
3. 实地考察:在实际场景中考察温度变化情况,了解实际温度需求。通过实地考察,我们可以更准确地掌握实际温度情况,为后续设定温度范围提供依据。
4. 综合分析:结合需求、标准和实地考察情况,综合分析确定合适的温度范围。在设定温度范围时,要考虑到设备的运行安全、产品质量、能源消耗等多方面因素。
三、确定合适的比例尺
1. 明确用途:确定比例尺的应用场景,如建筑设计、地图制作、工程图纸等。不同场景对比例尺的要求会有所不同,因此需针对不同场景进行比例尺的设定。
2. 了解实际尺寸:掌握实际物体的尺寸或实际距离,以便更好地应用比例尺。实际尺寸是确定比例尺的重要依据之一。
3. 选择合适的比例:根据用途和实际尺寸,选择合适的比例尺。比例尺的选择要考虑到图形的清晰度、精度要求、视觉效果等多方面因素。
4. 校验和调整:在应用比例尺后,要进行校验和调整,确保比例尺的准确性和适用性。如发现比例尺存在问题,需及时调整。
四、温度范围和比例尺的应用实例
1. 烹饪:在烹饪过程中,合适的温度范围对食物的口感和营养保持至关重要。如炒菜时需要控制火候,以保证食物的色泽和口感。而比例尺则可用于烹饪食材的配比,如制作蛋糕时,各种原料的比例需要精确控制。
2. 建筑设计:在建筑设计过程中,温度范围和比例尺都是非常重要的参数。设计师需要考虑到建筑物的热工性能,确定合适的温度范围以保证室内舒适度。而比例尺则用于绘制建筑图纸,确保建筑物的尺寸和布局符合设计要求。
3. 工业生产:在工业生产过程中,温度范围的控制对产品质量和生产安全具有重要影响。如钢铁冶炼、化工生产等行业,需要对温度进行精确控制。而比例尺则用于设备布局、管道连接等,确保生产流程的顺利进行。
五、总结
确定合适的温度范围和比例尺是许多领域中的关键任务。
我们需要根据实际需求、行业标准、实地考察和综合分析来确定合适的温度范围;同时,我们还要明确用途、了解实际尺寸、选择合适的比例并进行校验和调整来确定合适的比例尺。
只有准确把握温度范围和比例尺,才能更好地应对各种实际场景,保证产品质量、提高生产效率。
希望本文能读者在确定温度范围和比例尺方面提供有益的参考和指导。
判断:比例尺是一个比。
图上距离和实际距离的比叫比例尺所以比例尺是一个特殊的比,题目的话是对的。
如果你认可我的回答,请及时点击【采纳为满意回答】按钮,(或在客户端右上角评价点【满意】)你的采纳,是我前进的动力! 你的采纳也会给你带去财富值的。
如有不明白, 可以追问,直到完成弄懂此题!
比例尺问题
地图上的比例尺,表示图上距离比实地距离缩小的程度,因此也叫缩尺。
用公式表示为:比例尺=图上距离/实地距离。
比例尺通常有三种表示方法。
(1)数字式,用数字的比例式或分数式表示比例尺的大小。
例如地图上1厘米代表实地距离500千米,可写成:1∶50 000 000或写成:五千万分之一。
(2)线段式,在地图上画一条线段,并注明地图上1厘米所代表的实地距离。
(3)文字式,在地图上用文字直接写出地图上1厘米代表实地距离多少千米,如图上1厘米相当于地面距离10千米。
三种表示方法可以互换。
根据地图上的比例尺,可以量算图上两地之间的实地距离;根据两地的实地距离和比例尺,可计算两地的图上距离;根据两地的图上距离和实地距离,可以计算比例尺。
根据地图的用途,所表示地区范围的大小、图幅的大小和表示内容的详略等不同情况,制图选用的比例尺有大有小。
地图比例尺中的分子通常为1,分母越大,比例尺就越小。
通常比例尺大于二十万分之一的地图称为大比例尺地图;比例尺介于二十万分之一至一百万分之一之间的地图,称为中比例尺地图;比例尺小于一百万分之一的地图,称为小比例尺地图。
在同样图幅上,比例尺越大,地图所表示的范围越小,图内表示的内容越详细,精度越高;比例尺越小,地图上所表示的范围越大,反映的内容越简略,精确度越低。
地理课本和中学生使用的地图册中的地图,多数属于小比例尺地图。
地图比例尺 scale on map 地图上的线段长度与实地相应线段长度之比。
它表示地图图形的缩小程度,又称缩尺。
如1∶10万,即图上1厘米长度相当于实地1000米。
严格讲,只有在表示小范围的大比例尺地图上,由于不考虑地球的曲率,全图比例尺才是一致的。
通常绘注在地图上的比例尺称为主比例尺。
在地图上,只有某些线或点符合主比例尺。
比例尺与地图内容的详细程度和精度有关。
一般讲,大比例尺地图,内容详细,几何精度高,可用于图上测量。
小比例尺地图,内容概括性强,不宜于进行图上测量。
比例尺: 图上距离比实际距离的缩小程度.是图上距离/实际距离的比值. 比例尺越大,即图上距离代表的实际距离越长.能够反映的事物就越详细, 比例尺缩放的计算: 将原比例尺放大到n倍;原比例Xn 将原比例尺放大n倍;原比例X(n+1) 将原比例尺缩小到1/n;原比例X1/n 将原比例尺缩小1/n;原比例X(1-1/n) 比例尺缩放后,原面积之比变为缩放倍数的平方
七年级上策数学有理数加减法比较好的理解
理数运算是初中数学运算的重要基础,而我们要学习的有理数加减运算又是有理数运算的一部分。
下面,让我们一起来学习有理数加减法。
一、理解两个法则1、有理数加法法则:同号两数相加,取相同的符号,并把绝对值相加。
异号两数相加,绝对值相等时,和为0;绝对值不相等时,取绝对值较大加数的符号,并用较大的绝对值减去较小的绝对值。
一个数同0相加,仍得这个数。
根据有理数加法法则的叙述,在进行有理数加法运算时,先判断加法的类型,即是属于同号两数相加,还是属于异号两数相加,还是属于有一个加数是0。
然后依照法则去做。
为避免出错,在计算时,可以采取“先定符号,再定值”的原则,即根据法则先确定和的符号,再计算和的值。
其中“绝对值不相等的异号两数相加”的法则最难理解和掌握,符号的确定是哪个加数的绝对值大,和的符号就和哪个加数的符号相同;数值的确定是用较大的绝对值减去较小的绝对值,而不是较大数的绝对值减去较小数的绝对值。
二、掌握两个运算律小学里学过的加法交换律和加法结合律在有理数范围内仍然适用。
加法交换律:加法结合律:在进行有理数加减运算时,如能根据题目特点,合理、巧妙地运用运算律,将会使计算变得简单易解。
三、有理数加减混合运算有理数加减混合运算的基本步骤是:把算式中的减法转化为加法,如 可转化为 ,这就将原来的混合运算统一成加法运算,把算式看成几个正数和几个负数的和的形式。
上述算式还可以写成省略加号的和的形式,即 。
若把“+”、“-”看成性质符号,可读作 、 、 、 、 的和;若把“+”、“-”看成运算符号,可读作 减5减9加7加2。
然后结合运算律,简化计算出结果。
进行有理数的加减混合运算时应注意:① 交换加数的位置时,要连同符号一起交换。
② 在进行有理数加减运算时,不要盲目地计算,要注意观察题目的特点,恰当地运用运算律,达到简化的目的。
③ 有理数的和可以大于任何一个加数,也可以小于任何一个加数。
可以是正数,也可以是负数。
高防物理机,高防云服务器联系电话:13943842618